Have you ever stopped to truly think about something as common as a cube? It's more than just a simple shape; it’s a foundational piece of our physical world and, so, a pretty fascinating subject. From building blocks we played with as kids to complex puzzles that challenge our minds, this six-sided figure pops up everywhere. And there's one very specific thing about it that makes it stand out, something that gives it its distinct form and allows it to be so useful in so many different ways. It has a particular number of lines that make up its structure.
You know, it's almost a shape we take for granted, but its straightforward design hides some rather interesting characteristics. When you look at a cube, you're seeing a shape that’s got a very specific number of edges, and that number is what helps define it. It’s what makes it a cube and not some other kind of box or geometric form. This simple fact, that it has twelve of these connecting lines, is actually pretty important to how it behaves and how we can use it, in a way.
This particular attribute, the count of its edges, is what gives a cube its stability and allows it to fit together with other things so neatly. We're talking about the lines where two flat surfaces meet, and for a cube, there are, you know, exactly a dozen of these. This feature is a big part of why cubes are so common in everything from architecture to how we store things, and it's also why they make for such compelling puzzles. We'll explore just what this means and why it matters a little more here.
Table of Contents
- What Makes a Cube a Cube?
- Understanding the Structure: A Cube Has 12 Edges
- How Does a Cube with 12 Edges Fit into Our Everyday Life?
- The Challenge of the Scrambled Cube Puzzle and Its 12 Edges
- Can a Cube Solver Really Help with a Cube That Has 12 Edges?
- Exploring Other Cube-Like Puzzles Beyond the Standard "A Cube Has 12" Design
- Learning More About Cubes and Their Properties
- The Global Impact of One Special Cube with 12 Edges
What Makes a Cube a Cube?
When we talk about a cube, we're actually describing a particular kind of three-dimensional shape. It's a solid object that has six flat surfaces, which are all squares and are just the same size. This means it's a hexahedron, which, you know, simply means it has six faces. Each of these faces meets another at a line, and these lines are what we call edges. Then, where these edges come together, you find points, which we often refer to as corners or vertices. It's a pretty neat setup, actually, that gives it a very balanced look.
So, you might be wondering, what's so special about these particular features? Well, the fact that all its faces are identical squares and all its edges are the same length gives the cube a lot of symmetry. This means you can turn it around in many different ways, and it will still look exactly the same. This consistent form is why it's such a common shape in so many areas, from building things to, you know, even the way atoms sometimes arrange themselves. It's a shape that’s really quite stable and predictable.
Think about a simple dice, for instance. That's a cube. Every side is a square, and every edge is the same measure. This simple, yet powerful, geometric arrangement is what makes it, you know, a fundamental shape in mathematics and in our daily surroundings. It’s the very basis for how we think about space and volume, too. We often use it as a basic unit for measuring things, which is pretty cool when you stop to think about it.
Understanding the Structure: A Cube Has 12 Edges
Now, let's get down to one of the most defining features of a cube: its edges. As we mentioned, a cube has twelve of these connecting lines, and they are all, quite remarkably, just the same length. This particular count of twelve edges is what gives the cube its distinctive skeleton, so to speak. Imagine building a cube out of sticks; you would need exactly a dozen sticks of equal measure to form its outline. This number is not just a random figure; it's a direct result of having six square faces.
Each square face of a cube has four edges. If you were to just multiply 6 faces by 4 edges, you'd get 24, but that's not quite right. The reason is that each edge is shared by two different faces. So, you know, if you count them this way, you're counting each edge twice. That’s why you divide that number by two, which gives you the actual count of twelve distinct edges. This might seem like a small detail, but it's a fundamental part of what makes a cube what it is, actually.
These twelve edges also play a big part in how the cube holds its shape. They provide the framework, kind of like the beams in a house, ensuring that the cube stays rigid and doesn't collapse. This structural integrity is, you know, pretty important for anything from a storage box to a complex piece of machinery. The fact that a cube has 12 edges, all of them congruent, means it's a very balanced and sturdy shape, which is a big plus in many situations.
How Does a Cube with 12 Edges Fit into Our Everyday Life?
It's fascinating to consider just how often we encounter objects shaped like a cube, even if we don't always notice their twelve edges. Think about, for example, the sugar cubes you might put in your tea, or the ice cubes that cool your drinks. These are simple, everyday items that rely on the cube's stable form. Storage containers, too, often come in cube shapes because they can be stacked neatly, making the most of available space. This ability to pack together without wasted gaps is a direct benefit of its precise geometry, you know.
Beyond the kitchen, cubes show up in many other places. Building blocks for children are almost always cubes, helping young minds grasp concepts of space and structure. Even in the digital world, when you're looking at 3D graphics, many basic shapes are built from cubes or variations of them. They are, in some respects, the fundamental building blocks of many virtual environments. It's kind of amazing how such a simple shape can be so useful across so many different areas, really.
And then there's the Rubik's Cube, which is perhaps the most famous example of a cube in popular culture. This puzzle, with its shifting faces and, of course, its twelve main edges (though its internal structure is more complex), has captured the imagination of people all over the globe. It's a perfect illustration of how the cube's geometry can be turned into a challenge, one that tests our spatial reasoning and problem-solving skills. It just goes to show how versatile this shape truly is, doesn't it?
The Challenge of the Scrambled Cube Puzzle and Its 12 Edges
The Rubik's Cube is, arguably, the ultimate representation of a cube as a puzzle. What makes it so compelling is the way its parts move around those central axes, creating a jumbled mess that you then have to sort out. When you're trying to figure out a scrambled cube puzzle, you're essentially trying to reverse a series of rotations to get all the colors back to their correct sides. The twelve edges of the main cube, while not directly moved as individual pieces, define the overall structure within which the colored squares shift. It's a very clever design, actually.
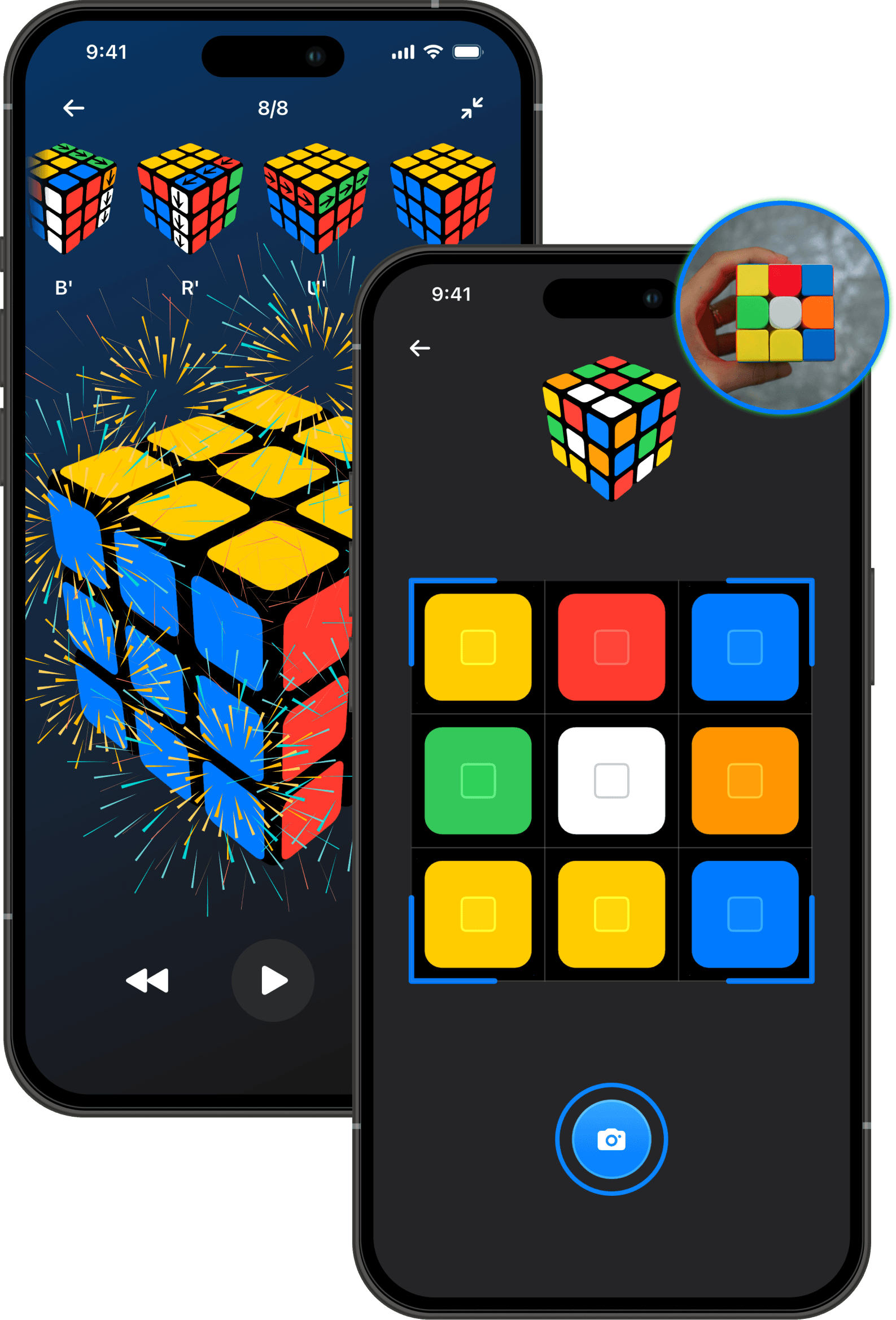
Our source text mentions that you can "calculate the solution for a scrambled cube puzzle in only 20 steps." This is pretty impressive, isn't it? It means that even the most mixed-up cube can be put right in a relatively small number of moves. The process usually involves setting up the pattern you see on your mixed-up cube, perhaps using a color picker to mark the squares on an online tool. Then, you simply press a button to find the way to fix it, and the system gives you instructions to follow. This makes solving a cube, which might seem very hard, actually quite approachable for anyone.
The idea of a "scramble pattern" is just a fancy way of saying how messed up your cube is. To find the path to the solution, you need to tell the solver exactly what your cube looks like. The solver then figures out the rotations that will lead to the solution. It's pretty cool how technology can take something that seems so complex and break it down into simple, step-by-step instructions. This helps people who are new to cube solving, and it's also a neat way to learn more about how the cube works, really.
Can a Cube Solver Really Help with a Cube That Has 12 Edges?
Absolutely, a cube solver can be a real game-changer for anyone struggling with a scrambled puzzle, especially the classic 3x3x3 cube that, you know, clearly has its twelve edges defining its form. The source text points out that "it's very easy to use our free 3d rubik's cube solver, simply fill in the colors and click the solve button." This takes away a lot of the frustration that comes with trying to figure out the puzzle on your own. It's like having a personal tutor for your cube, guiding you through each turn.
These online tools aren't just for the standard 3x3x3 cube, either. Our source mentions "online rubik's cube, 4x4x4 and other nxnxn cube solver and simulator." This means whether you're working with a smaller cube, a bigger one, or something in between, there's likely a tool to help you out. You can set up the scramble you have, and the solver will provide the rotations you need to get to the solution. It’s pretty convenient, and it makes the world of cube puzzles much more open to everyone, too.
The core idea behind these solvers is to break down the complex problem of a scrambled cube into a series of manageable steps. By knowing the precise rotations, you can, you know, systematically work your way back to the solved state. It's a practical application of the cube's mathematical properties, showing how its inherent structure, including its twelve edges, allows for such precise calculations. It really takes the guesswork out of solving, making it a fun activity rather than a frustrating one.
Exploring Other Cube-Like Puzzles Beyond the Standard "A Cube Has 12" Design
While the classic 3x3x3 Rubik's Cube is probably the most famous, the world of cube-like puzzles is, you know, actually much bigger. The source text mentions "Play dozens of our free 3d puzzle models or use any of our 3d puzzle solvers!" This suggests there's a whole collection of different kinds of puzzles, many of which are variations on the cube theme. Some might have more faces, or different shapes, but they often build on the same principles of rotation and rearrangement that the standard cube uses.
For instance, a 4x4x4 cube, also known as the Rubik's Revenge, is a good example of a puzzle that takes the basic cube concept and makes it more complex. While it still has a core structure that could be related to twelve main edges, its internal mechanics are more involved, with more pieces to move and align. These larger cubes require different strategies and a deeper understanding of how the pieces interact. It's a fascinating progression for those who have, you know, mastered the standard cube.
These varied puzzles, whether they are bigger cubes or other geometric shapes, all rely on the idea of moving parts around a fixed center to achieve a desired pattern. They challenge our spatial awareness and our ability to plan multiple steps ahead. They are, in a way, like advanced versions of the simple cube, pushing the boundaries of what a puzzle can be while still retaining that fundamental charm of physical manipulation. It's pretty neat how many different kinds of challenges can come from one basic idea.
Learning More About Cubes and Their Properties
There's a lot more to learn about cubes than just their role in puzzles. Our source text encourages us to "learn everything you need to know about cubes, including their properties, formulas for volume and surface area." This points to the cube's significance in mathematics and how we describe the world around us. Understanding a cube's properties means knowing about its faces, edges, and corners, and how they all relate to each other. It’s a bit like learning the basic grammar of shapes, you know.
The formulas for volume and surface area are, you know, very practical applications of this knowledge. Volume tells you how much space a cube takes up or how much it can hold, which is pretty useful for things like packing boxes or designing rooms. Surface area, on the other hand, tells you the total area of all its outer faces. This is important for things like painting a cube or wrapping a gift. These simple calculations are a direct result of the cube's consistent and predictable shape, including the fact that it has 12 edges of equal measure.
The text also says, "Let’s explore the properties and the role of the cube in mathematics and in real life." This really highlights how interconnected these ideas are. Cubes aren't just abstract concepts in a textbook; they are fundamental to how we build, design, and even understand the natural world. From the structure of crystals to the way we organize data, the cube's simple yet powerful geometry is, you know, constantly at play. It's pretty cool to see how such a basic shape has such far-reaching influence.
The Global Impact of One Special Cube with 12 Edges
It's truly remarkable to think about the impact of the Rubik's Cube. The source text states, "There is only one rubik’s cube and it changed the world." This might seem like a big statement, but when you consider how widely it spread and how many people it influenced, it’s not much of an exaggeration. It became a worldwide phenomenon, a puzzle that transcended language and culture, captivating millions. It showed people that complex problems could be solved with logic and persistence, and it sparked a global interest in puzzles and spatial reasoning, too.
The Rubik's Cube, with its seemingly simple cube form and its twelve edges, encouraged a generation to think differently about challenges. It wasn't just a toy; it was a mental workout, a way to train your brain. It led to speedcubing competitions, where people try to solve the puzzle in mere seconds, pushing the limits of human dexterity and memory. This competitive aspect added another layer to its popularity, making it more than just a casual pastime, in a way.
The enduring legacy of the Rubik's Cube is clear. It continues to be a beloved puzzle, a symbol of clever design and intellectual challenge. Our source invites us to "Make your move today and start your rubik’s cube journey" and to "Find everything you need to know about the rubik’s cube right here." This shows that the journey of discovery with the cube is still very much alive. It’s a reminder that even a shape as simple as a cube, defined by its twelve edges, can hold endless possibilities for learning and fun. It's pretty inspiring, honestly.